Matrix Inverse [Matrix Functions]

Functions
arm_status	arm_mat_inverse_f32 (const arm_matrix_instance_f32 *pSrc, arm_matrix_instance_f32 *pDst)

---

Detailed Description

Computes the inverse of a matrix.

The inverse is defined only if the input matrix is square and non-singular (the determinant is non-zero). The function checks that the input and output matrices are square and of the same size.

Matrix inversion is numerically sensitive and the Cortex-R4 DSP library only supports matrix inversion of floating-point matrices.

Algorithm

The Gauss-Jordan method is used to find the inverse. The algorithm performs a sequence of elementary row-operations till it reduces the input matrix to an identity matrix. Applying the same sequence of elementary row-operations to an identity matrix yields the inverse matrix. If the input matrix is singular, then the algorithm terminates and returns error status ARM_MATH_SINGULAR.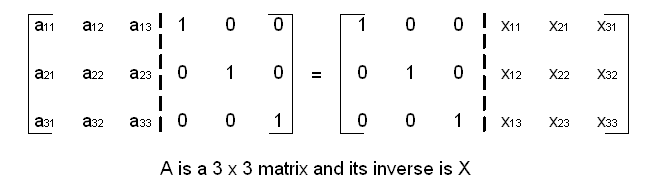

Matrix Inverse of a 3 x 3 matrix using Gauss-Jordan Method

---

Function Documentation

arm_status arm_mat_inverse_f32	(	const arm_matrix_instance_f32 *	pSrc,
		arm_matrix_instance_f32 *	pDst
	)

Floating-point matrix inverse.

Parameters:

[in]	*pSrc	points to input matrix structure
[out]	*pDst	points to output matrix structure

Returns:

The function returns ARM_MATH_SIZE_MISMATCH if the input matrix is not square or if the size of the output matrix does not match the size of the input matrix. If the input matrix is found to be singular (non-invertible), then the function returns ARM_MATH_SINGULAR. Otherwise, the function returns ARM_MATH_SUCCESS.

Examples:

arm_matrix_example_f32.c.

Definition at line 68 of file arm_mat_inverse_f32.c.